APPENDICE 3

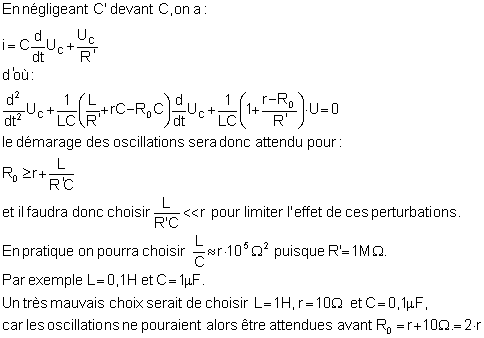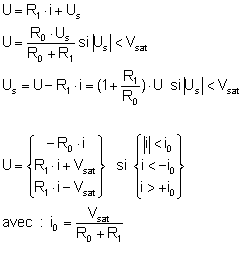
Oscillations libres entretenues dans un circuit rLC

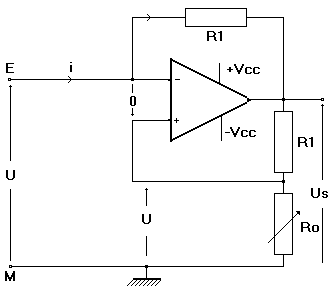
On utilise un montage à résistance négative à amplificateur opérationnel.

Étude du montage à résistance négative :

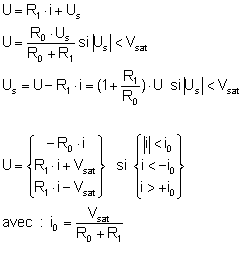
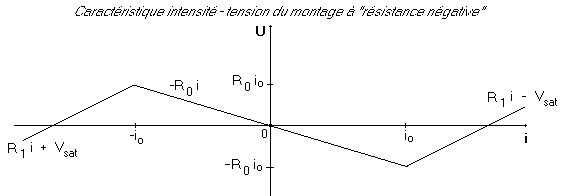
Équations différentielles du circuit :

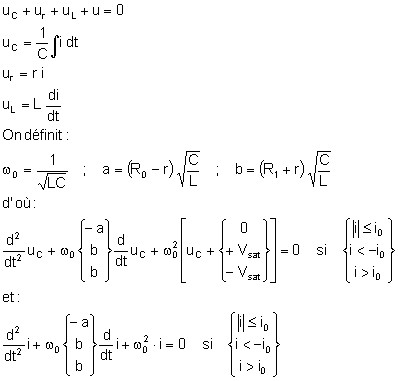
Équation réduite pour le courant :

Quelques résultats de simulation numérique

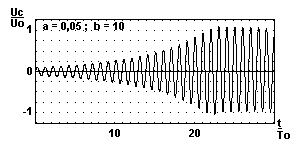
Démarrage et stabilisation des oscillations :

Méthode de Runge-Kutta sur calculatrice TI92+ (dt = 0,01T₀ ; i(0) = 0,1i₀).

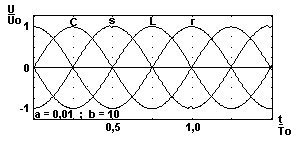
Oscillations entretenues :

Méthode de Runge-Kutta sur calculatrice TI92+ (dt = 0,005T₀ ; i(0) = i₀).

C’est la tension aux bornes du condensateur qui est la plus proche d’un signal sinusoïdal, surtout si le paramètre "a" n’est pas négligeable

Les déformations des signaux sont directement reliées à la forme de la caractéristique intensité - tension du montage à résistance négative et non à des " parasites " dans le circuit réel.

On se contentera donc obligatoirement dans l’étude du circuit réel de visualiser la tension aux bornes du condensateur et ce uniquement pour R₀ » r (a << 1).
Les tensions U_L et U_r ne sont bien sur pas " séparables " dans le circuit réel, mais en général U_r est négligeable devant U_L.
U_r est proportionnelle au courant dans le circuit.
On remarque les différents déphasages.

Remarque :

Dans les programmes français (95) de Terminale S, il est proposé, en activités expérimentales, de remplacer la caractéristique réelle du montage à résistance négative par une caractéristique " continûment dérivable " pour obtenir une équation différentielle du type Van der Pol. Équation qui est ensuite résolue numériquement. Ceci n’est pas cohérent car :

la résolution numérique de l’équation discontinue réelle est aussi simple et plus directe que celle de Van der Pol,

l’intérêt de cette modélisation est de rechercher l’évolution des solutions " sur le papier " et non pas d’utiliser des méthodes numériques !

les résultats obtenus ne reproduisent la réalité que très partiellement (on perd toutes les déformations que l’on risque d’observer dans l’expérience réelle).

Exemple de résolution sur calculatrices TI89/TI92+ :

Ces calculatrices à microprocesseur 68000 possèdent un solveur numérique de systèmes d’équations différentielles linéaires du premier ordre. Ce solveur utilise au choix les méthodes d’Euler ou de Runge - Kutta. Sachant qu’une équation différentielle linéaire du deuxième ordre peut se transformer en un système de deux équations différentielles linéaires du premier ordre, il est alors très simple de " simuler " toutes les tensions dans le circuit…

Dans l’exemple qui suit et présentant quelques écrans de la TI92+ :

y1 et c2 représentent U_c/U₀,

y2 et c3 représentent i/i₀,

y3/2p et c4 représentent U_L/U₀,
c5 = -c2 – c3 – c4 représente U_s/U₀,
toutes les tensions sont normalisées à 1,
toutes les périodes sont égales à 1,
toutes les fréquences angulaires sont égales à 2p.

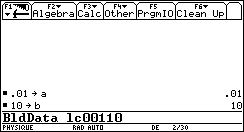
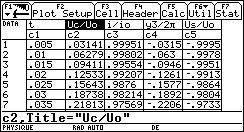
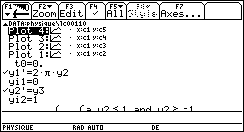
Schéma réel de fonctionnement lors du branchement d’un oscilloscope aux bornes du condensateur :

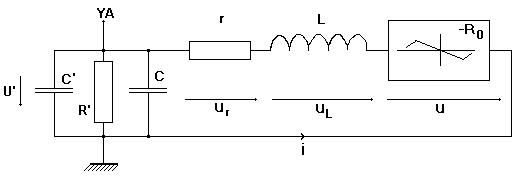
Utiliser un oscilloscope pour visualiser les tensions dans le circuit n’est pas sans conséquence en raison de son impédance d’entrée non infinie.

L’entrée (DC) de l’oscilloscope étant équivalente à une résistance R’ = 1 MW en parallèle avec un condensateur C’ de 16 à 47 pF, il faut tenir compte de ces valeurs :

il est important de choisir C >> 50 pF,
le démarrage des oscillations ne pourra pas être obtenu pour R₀ = r.

Équation différentielle du circuit réel hors saturation :