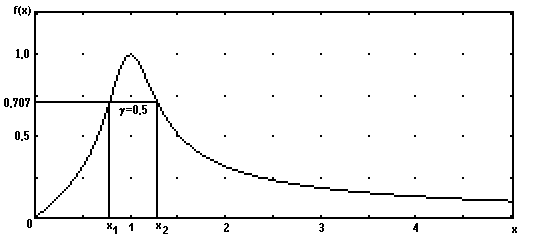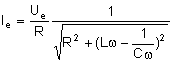
Courbes théoriques de résonance d’intensité
Courbe réduite :
L’intensité efficace Ie dans un circuit RLC série excité par une tension alternative sinusoïdale de valeur efficace Ue et de pulsation w est donnée par :
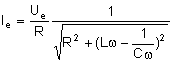
Si l’on définit la fréquence réduite x par :
![]()
et la "largeur" de résonance
g comme l’inverse du facteur de qualité Q :![]()
alors, l’expression devient :
![]()
il suffit donc d’étudier la fonction f(x) sans dimension :
![]()
Cela peut aisément se faire avec une calculatrice graphique. Par exemple avec une TI92 pour des largeurs
g de 0,1 ; 1,0 ; 10 :

Bande passante à 3 dB :

On justifie ici que
g = x2 – x1 est la " largeur " de la résonance.Remarque :
Si l’on avait étudié les courbes de puissance f2(x), alors
g serait la " largeur à mi-hauteur " de la courbe de Lorentz et l’on aurait écrit dB = -10 log (P/Pm) = -10 log f2 = -20 log f ; les décibels vrais concernent les puissances mais peuvent être calculés aussi à partir des intensités en remplaçant le facteur 10 par un facteur 20.Exemple : facteur de qualité égal à 2
On a donc une largeur
g = 0,5 et x1 = 0,78 et x2=1,28